快速傅里叶变换（FFT）

复数

基本定义

我们对于实数域 $\R$ 进行扩充，因为我们注意到对于方程 $x^2=-1$，我们无法在 $\R$ 内无法找到一个解。但是，我们总是相信一个 $n$ 次方程 $f_n(x)=0$ 总会有 $n$ 个解。因此，我们对于实数域进行扩充，计 $i^2=-1$，即可以用 $z=a+bi$ 的形式来描述一个数，我们称这样的数叫做复数 (Complex)，记作 $\Complex$。

对于一个新的数域，我们需要定义一个加减乘除与之对应，特殊地，对于 $b=0$ 的情况，也即 $z\in \R$ 时，需要满足实数和复数在这些运算上的一致性，同时，我们也希望复数的加减乘除满足交换、结合律等法则。

于是，我们得到了定义：

$z_1=a+ bi,z_2=c+ di$，则 $z=z_1\pm z_2=(a+ c)\pm(b+ d)i$。
$z_1=a+bi,z_2=c+di$，则 $z=z_1\cdot z_2=(a+bi)\cdot(c+di)=(ac-bd)+(ad+cb)i$。

复数的表示

普通表示

这就是我们经常用的 $z=a+bi$ 的方式。这是最朴素的代数表示方法，虽然简单，但有的时候进行乘除操作时因多项式乘法会导致很多冗余的项，因此，我们希望一些更加具有鲜明几何意义的表示方法。

复平面

我们发现，一个复数只需要两个参量就可以被决定。例如有序数对 $(x,y)$ 就可以表示一个复数 $x+yi$。不难得到，所有的二元组 $(x,y)$ 都可以一一对应一个复数。这个二元组不难让我们联想到坐标系下的点，于是，我们有了复平面。

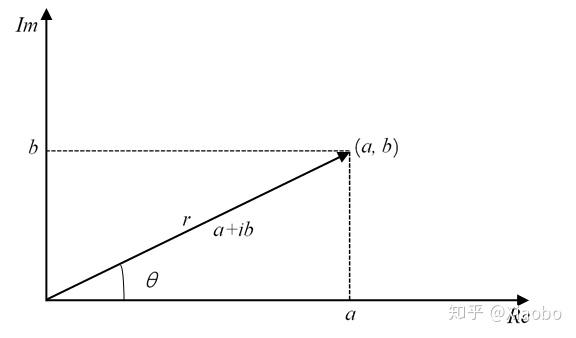
如图，我们定义横向的坐标轴为 **实轴 (Real)**，而纵向的坐标轴为 **虚轴 (Imagination)**，于是一个点 $(a,b)$ 就可以唯一地表示一个复数 $a+bi$，横坐标对应实部，纵坐标对应虚部即可。而我们又知道，坐标系内的一个点又可以唯一地对应一个向量 $\vec{r}$，因此，我们又知道一个复数 $a+bi$ 又可以使用向量 $\vec{r}=(a,b)$ 来表示。

由此，我们知道了向量在复平面上的几何意义。进而，我们又可以引申出来一些概念：

复数的模，类似于向量，我们定义 $z=a+bi$ 的模 $|z|=\sqrt{a^2+b^2}$.
负数的幅角，在复平面中，我们定义向量 $(a,b)$ 表示的复数 $a+bi$ 的幅角 $\theta$ 的正切值 $\tan \theta=\frac{b}{a}$，也就是说，$\theta=\arg (a,b)$。

三角表示

我们已经知道了复数可以表示成向量，类似向量，我们也可以用三角函数表示复数。

具体地，对于 $\vec{r}=(a,b)$，我们计 $|r|=r$，$\arg r=\theta$，那么根据复平面不难得出，$\vec{r}=|r|(\cos \theta +i\sin \theta)$。

根据三角表示，我们推导乘法法则，不难得到：

$$|r_1|(\cos \theta_1+i\sin \theta_1)\times|r_2|(\cos \theta_2+i\sin \theta_2)=|r_1||r_2|(\cos (\theta_1+\theta_2)+i\sin(\theta_1+\theta_2))$$

也就是说，复数乘法的几何意义就是辐角相加，模相乘。

指数表示

欧拉公式

$$e^{ix}=\cos x+i\sin x$$

我们发现括号内与三角表示一样，因此，复数 $\vec{r}=(a,b)=r(\cos \theta+i\sin \theta)=r\times e^{i\theta}$。

单位根

对于 $n$ 次方程 $x^n=1$，我们不难得到在 $\Complex$ 内可以得到 $n$ 个解，可以表示为 $w_n^k,k\in [0,n-1]$。其中 $w_n^1=\cos \frac{2\pi}{n}+i\sin \frac{2\pi}{n}$，相应地，$w_{n}^k=(w_{n}^1)^k=e^{i\frac{2k\pi}{n}}$。于是，在复平面上，这些根可以看成是平分单位圆的 $n$ 条半径。它们具有以下性质：

$w_{2n}^{2k}=w_{n}^k$。这通过指数表示可以很方便得得出。
$w_{n}^{k+\frac{n}{2}}=-w_{n}^{k}$。这里可以看作是绕单位圆绕了半圈（$\frac{2\frac{n}{2}\pi}{n}=\pi$）。

傅里叶变换

这里我们只给出傅里叶变换的式子，至于式子与快速傅里叶变换的关系，我们在 快速傅里叶变换 的章节中再详细说明。

对于多项式 $f=\sum\limits_{i=0}^nf_ix^i$，我们进行变换：

$$y_k=\sum\limits_{i=0}^n f_ie^{i\frac{2\pi}{n}ki}$$

或者，对 $y_n$ 进行傅里叶逆变换：

$$c_k=\sum\limits_{i=0}^n f_ie^{-i\frac{2\pi}{n}ki}$$

我们称这样的变换为 离散傅里叶(逆)变换。

正文

多项式乘法思路

多项式乘法有两种实现方式。第一种是用多项式的系数表示法，也即用 $(f_0,f_1,f_2,\dots,f_n)$ 表示一个多项式 $f$，于是不难得到 $f=h\times g$ 的系数可以表示为

$$f_k=\sum\limits_{i=0}^kh_ig_{k-i}$$

于是枚举 $k$ 和 $i$ 一共需要 $O(n^2)$ 的复杂度。

还有一种方法是点值表示，如果我们知道 $n+1$ 个点 ${(x_0,y_0),(x_1,y_1),\dots,(x_n,y_n)}$ 表示一个多项式 $f$，那么函数 $f=g\times h$ 可以表示为 ${(x_0,h_0\times g_0),(x_1,h_1\times g_1),\dots,(x_n,h_n\times g_n)}$。这样乘法的复杂度就是 $O(n)$，但是将系数表示转换成点值表示也需要枚举点并且 $O(n)$ 计算，也需要 $O(n^2)$ 的复杂度。

一时间我们想不到优化两种方法的方法，但是，我们想想是不是可以利用自变量的一些性质来快速求点值？

在实数范围内，我们似乎找不到具有特殊性质的自变量，但是，我们把目光投向了虚数，单位根。

对于多项式 $f=f_0+f_1x+f_2x^2+f_3x^3+f_4x^4+f_5x^5+f_6x^6+f_7x^7$，我们考虑分治，将次幂的奇偶性作为标准进行分类，即：

$$f=(f_0+f_2x^2+f_4x^4+f_6x^6)+(f_1x+f_3x^3+f_5x^5+f_7x^7)$$

$$=(f_0+f_2x^2+f_4x^4+f_6x^6)+x(f_1+f_3x^2+f_5x^4+f_7x^6)$$

我们设：

$$g(x)=f_0+f_2x+f_4x^2+f_6x^3$$

和

$$h(x)=f_1+f_3x+f_5x^2+f_7x^3$$

于是 $f=g(x^2)+x\times h(x^2)$。我们将 $w_n^k$ 和 $w_n^{k+\frac{n}{2}}$ 得到：

$$f(w_n^k)=g(w_{n}^{2k})+w_{n}^kh(w_n^{2k} )$$

$$f(w_n^{k+\frac{n}{2}})=g(w_{n}^{2k+n})+w_{n}^{k+\frac{k}{2}}h(w_{n}^{2k+n})$$

根据单位根的性质，不难得到