网络流
网络流
基本概念
我们现在有一张图 $G={V,E}$,对于每一条边 $e\in E$,我们用 $(u,v,w)$ 来描述它,分别代表起点,终点和边权;并且这张图上有一个起点 $s$ 和一个终点 $t$,那么我们就可以称这个图是一张 网络。
另外的,对于这个起点 $s$,我们称之为 源点,对于终点 $t$,我们称之为 汇点。下面讲网络流几个基本概念。
弧
对于每一条边 $e=(u,v,w)\in E$,我们称之为 弧。而这里的 $w$ 被称为这条弧的容量。
流
对于一条 $u\to \dots \to v$ 的简单路径,我们称这是这张网络的一个 流。它满足以下性质:
- 对于流 $v_1\to\dots\to v_n$,它的大小必须小于等于 $\min\limits_{i=1}^{n-1}{w_{(v_i,v_{i+1})}}$。也就是说,流的大小小于等于路径上所有容量的最小值。
- 对于除源点和汇点之外的所有节点,总满足流进总流量等于流出总流量。
对于一张网络,我们希望给定一个确定的流,使得汇点的流量最大,这个问题叫做 最大流问题。
割
对于一个网络 $G=(V,E)$,我们将集合 $V$ 分成两份,变成 $S$ 和 $T$,其中 $s\in S,t\in T$,并且满足 $S\cup T=V,S\cap T=\emptyset$,则称这一种划分方式是这个网络的一个 割。而 最小割问题 就是希望找到一个割,使得 $\sum\limits_{u\in S,v\in T}w_{u,v}$ 最小。
残余网络
对于一个网络,如果我们已经在这张网络上进行了流的操作,则称流之后的网络为 残余网络。
最大流
FF算法 (Ford-Fulkerson)
算法过程
算法的基本思路是,对于一张残余网络,我们总找到一条 增广路 使得总流量增加。而对于顺序不对的情况,我们使用反向边来实现 反悔 的操作。
增广路
对于一个流 $f=(s\to\dots\to t)>0$,则我们称这个流 $f$ 是该网络的一条增广路。简单来说,就是使总流量增加的路径。
于是找增广路就非常好实现,我们主要来看看怎么实现 反悔 操作。
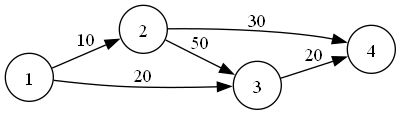
如图网络。显然,对于这张网络,最大流就是 $10+20=30$,但是如果我们先流 $1\to 2\to 3\to 4$ 这一条路径,那么残余网络就变成:
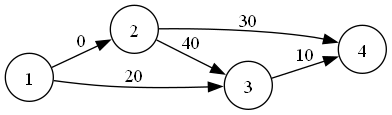
然后流完 $(1\to 3\to 4)$ 之后就没了,得出来的最大流变成了 $20$。显然,这是我们流的顺序不当导致的。如何避免这种情况呢?我们考虑在每一条单向边顺带着连一条反边。如图:
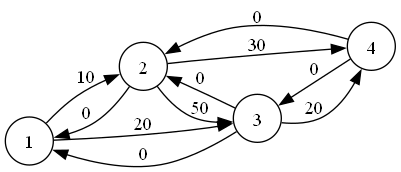
由图可知,这些 反边 的容量初始是 $0$,额外的,我们在进行增广的时候,我们在减小正向边容量的同时增大反向边容量,比如对路径 $(1\to 2\to 3\to 4)$ 进行增广后,得到图:
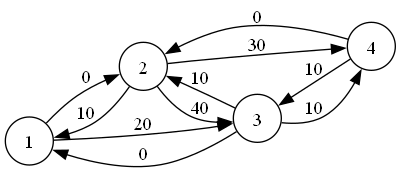
可以看到,我们在进行一次增广之后,把反向边都加上了流量大小的容量,这就是接下来我们实施 反悔 操作的重要步骤。进行这一步操作之后,我们继续跑网络流,比如 $(1\to 3\to 4)$:
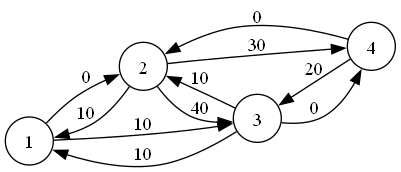
然后,我们惊奇的发现,这张图竟然还可以进行增广操作,也就是 $(1\to 3\to 2\to 4)$ 这一条增广路。于是增广之后,我们得到下图:
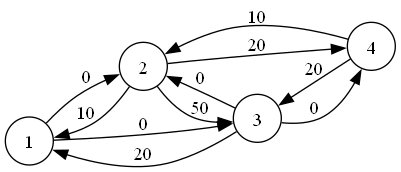
于是,我们这样得到的最大流就是 $30$。
对比原图,我们发现这个图的最终结果和直接增广 $(1,2,4)$ 和 $(1,3,4)$ 两条路径没有任何区别。也就是说,我们通过反悔操作,把我们以前的流不优时再流回去,实际上并不会对答案造成影响。这样,我们就把 $\text{FF}$ 算法学完了。
复杂度分析
对于一次增广操作,它的复杂度是 $O(E)$,而这样的增广最多进行 $O(f)$ 次,这里 $f$ 就是最大流。这种情况发生在每次增广只能增加 $1$ 的情况。因此,$\operatorname{FF}$ 算法的时间复杂度上限为 $O(|E|f)$。
$\text{EK}$ 算法
对于增广操作,我们也可以使用 $\operatorname{BFS}$ 完成每一次的增广操作。就是在残余网络中找到一个单轮的最大流,然后不断增广直至不能增广。这个算法在实际应用中并不广泛,因此了解思路即可。
$\operatorname{EK}$ 时间复杂度证明
这里我引用 $\text{oi-wiki.org}$ 中的证明,因为实在是太麻烦且没有必要了。
增广总轮数的上界的证明
首先,我们引入一个引理——最短路非递减引理。具体地,我们记 $d_f(u)$ 为 $G_f$ 上结点 $u$ 到源点 $s$ 的距离(即最短路长度,下同)。对于某一轮增广,我们用 $f$ 和 $f’$ 分别表示增广前的流和增广后的流,我们断言,对于任意结点 $u$,增广总是使得 $d_{f’}(u) \geq d_f(u)$。我们将在稍后证明这一引理。
不妨称增广路上剩余容量最小的边是饱和边(存在多条边同时最小则取任一)。如果一条有向边 $(u, v)$ 被选为饱和边,增广会清空其剩余容量导致饱和边的消失,并且退流导致反向边的新增(如果原先反向边不存在),即 $(u, v) \not \in E_{f’}$ 且 $(v, u) \in E_{f’}$。以上分析使我们知道,对于无向边 $(u, v)$,其被增广的两种方向总是交替出现。
在 $G_f$ 上沿 $(u, v)$ 增广时,$d_f(u) + 1 = d_f(v)$,此后残量网络变为 $G_{f’}$。在 $G_{f’}$ 上沿 $(v, u)$ 增广时,$d_{f’}(v) + 1 = d_{f’}(u)$。根据最短路非递减引理又有 $d_{f’}(v) \geq d_f(v)$,我们连接所有式子,得到 $d_{f’}(u) \geq d_{f}(u) + 2$。换言之,如果有向边 $(u, v)$ 被选为饱和边,那么与其上一次被选为饱和边时相比,$u$ 到 $s$ 的距离至少增加 $2$。
$s$ 到任意结点的距离不可能超过 $|V|$,结合上述性质,我们发现每条边被选为饱和边的次数是 $O(|V|)$ 的,与边数相乘后得到增广总轮数的上界 $O(|V||E|)$。
接下来我们证明最短路非递减引理,即 $d_{f’}(u) \geq d_f(u)$。这一证明并不难,但可能稍显绕口,读者可以停下来认真思考片刻。
最短路非递减引理的证明
考虑反证。对于某一轮增广,我们假设存在若干结点,它们在该轮增广后到 $s$ 的距离较增广前减小。我们记 $v$ 为其中到 $s$ 的距离最小的一者(即 $v = \arg \min_{x \in V, d_{f’}(x) < d_f(x)} d_{f’}(x)$)。注意,根据反证假设,此时 $d_{f’}(v) < d_f(v)$ 是已知条件。
在 $G_{f’}$ 中 $s$ 到 $v$ 的最短路上,我们记 $u$ 是 $v$ 的上一个结点,即 $d_{f’}(u) + 1 = d_{f’}(v)$。
为了不让 $u$ 破坏 $v$ 的「距离最小」这一性质,$u$ 必须满足 $d_{f’}(u) \geq d_f(u)$。
对于上式,我们令不等号两侧同加,得 $d_{f’}(v) \geq d_f(u) + 1$。根据反证假设进行放缩,我们得到 $d_f(v) > d_f(u) + 1$。
以下我们尝试讨论 $(u, v)$ 上的增广方向。
假设有向边 $(u, v) \in E_f$。根据 $BFS$「广度优先」的性质,我们有 $d_f(u) + 1 \geq d_f(v)$。该式与放缩结果冲突,导出矛盾。
假设有向边 $(u, v) \not \in E_f$。根据 $u$ 的定义我们已知 $(u, v) \in E_{f’}$,因此这条边的存在必须是当前轮次的增广经过了 $(v, u)$ 并退流产生反向边的结果,也即 $d_f(v) + 1 = d_f(u)$。该式与放缩结果冲突,导出矛盾。
由于 $(u, v)$ 沿任何方向增广都会导出矛盾,我们知道反证假设不成立,最短路非递减引理得证。
(这个证明比我前面写的加起来还长)
$\operatorname{Dinic}$ 算法
考虑提前进行 $BFS$ 分层,然后使用 $DFS$ 跑增广路。具体地,我们跑 $BFS$,给每一个 $v\in V$ 一个 $dep$ 表示到源点 $s$ 的最短距离。然后,在 $DFS$ 的时候,我们的增广路 $v_1 \to \dots\to v_n$,对于 $\forall i\in[1,n-1]$,总存在 $dep_i=dep_{i+1}-1$。也就是说,对于一个点 $u$,我们只流给它的下一层。因此,我们称这个分完层之后的残余网络为 $G=(V,E)$ 网络的一个层次图。而我们称在这张图上的最大增广为 阻塞流。
我们希望一次求出整张层次图的最大流,因此我们就需要多路增广。但是,对于每一次搜到一个点,可能前面的路径已经流完了,必须从当前的弧开始,因此,我们可以到一个点记录一下现在这个点流到了第几个弧,然后再流到这个点的时候就可以从上次没流完的开始流。这个常数优化我们称为当前弧优化。
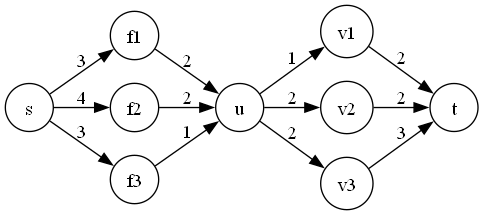
如图,模拟网络流过程,从 $(s\to f_1\to u)$ 进行增广,于是 $u$ 获得流量 $2$,然后把这些流量进行分配,也即 $(u\to v_1\to 1)$ 流过 $1$,$u\to v_2\to 1$ 流过 $1$。无法继续增广,于是,返回 $s$ 节点,通过 $(s,f_2,u)$ 给 $u$ 大小为 $2$ 的流量。注意,此时,$u$ 就不用流到 $v_1$ 了,继续流没有流完的 $v_2$ 即可。因此,这里就体现出了当前弧优化。
代码也非常简单:
1 | int n,m,s,t; |
最大流问题中,基本上 $\text{Dinic}$ 就很够用了,但还有一个 $\text{Dinic}$ 的常熟优化版本:$\operatorname{ISAP}$,这种算法只需要在 $dfs$ 之前进行一遍 $BFS$ 分层。但是,$BFS$ 的复杂度是 $O(|E|)$,而一遍 $DFS$ 是 $O(|E||V|)$,所以优化极小。
最小割
我们之前已经说过最小割问题的定义,我们现在就来讨论怎样完成这个问题。
首先,看一个定理:
最大流最小割定理
对于一张网络 $G=(E,V)$,它的最大流为 $f$,最小割为 $|S,T|$,则有 $f=|S,T|$。
这个定理直接指出了最大流与最小割之间的关系,我们对于最小割的研究也就很方便了。
关于证明,这里从略,有兴趣可以去看 $\text{oi-wiki}$ 上的详细证明。
最小费用最大流
Warning
这里是在保证 最大流 的基础上进行最小费用操作的。
具体地,对于每一条弧 $(u,v)$,我们不仅有一个 $w$ 容量,而且还有一个单位容量花费 $cost$,也就是说,如果有一个流 $f$ 流过这条弧,那么会产生 $f\times cost$ 的花费,要求最大流的前提下最小化花费。
首先要明确,一条增广路上的花费为 $f\sum\limits_{e\in E} cost_e$。这很好理解,因为每经过一条弧就要加上 $f\times cost$ 的费用,一共就是 $f\times \sum\limits_{e\in E}cost_e$ 的花费了。
我们惊奇的发现一条路径上花费只与流量和单位花费有关,而因为最大流是一定的,所以我们只需要最小化 $\sum\limits_{e\in E}cost_e$ 即可。因此,我们可以进行贪心求解,也就是每一次求出费用和最小的增广路进行增广,到最后费用就一定最小了。其中,值得注意的是,我们对于路径 $(u,v,w,cost)$ 的反边需要设置成 $(v,u,0,-cost)$。也就是说,在反悔的时候,一定是费用再倒退回去。这也给我们一个启示:虽然容量不能为负,但是费用可以。
而求最短路的过程,我们选择使用 $SPFA$,因为虽然它的复杂度不对,但是仍然是在不卡的时候很有力的工具。而不适用 $n\log n$ 的 $dijkstra$ 的原因是它无法处理负边。但是我们仍然可以使用一些特殊手段来处理负边,比如使用 $Johnson$ 全源最短路算法中的是能思想。
1 | queue<int> q; |
经典建模套路
拆点
在网络流中,往往有这样一个限制:每个状态只能选择一次,或者每个状态只能贡献一次。对于这种数量的限制,我们就可以使用拆点来实现。
只能选择一次
对于这种问题,我们把一个点 $i$ 拆成 $i$ 与 $i+n$ 两个点,如图所示:
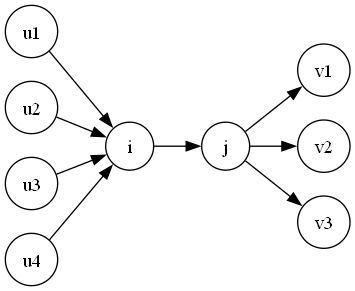
其中 $j=i+n$。注意,这里 $i$ 作为入点,以前所有连向 $i$ 的边都连向 $i$,然后 $j$ 作为出点,以前所有从 $i$ 出发的都由 $j$ 往外出发。而在 $i\to j$ 中间也连一条边,其中这条边容量为 $0$,这样我们就已经保证了 $i$ 只允许被遍历一遍。
只能贡献一次
对于这个问题,我们就要考虑费用流了。显然,我们是无法只使用最大流来约束双重状态的。因此,这一次仍然是把 $i$ 拆成 $i$ 和 $i+n$,但是连边不一样,如图:
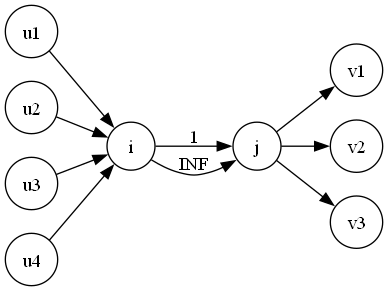
注意到,这一次我们在 $i,i+n$ 之间连了两条边,其中一条是 $(i,i+n,1,a)$,另一条是 $(i,i+n,INF,0)$。其中 $a$ 表示贡献。这就是说,从 $i$ 到 $i+n$ 有两种路线,第一种是拿贡献的,第二种是不拿的,显然在跑最大费用最大流的时候会优先选择第一种路线,这样我们就跑出来了最大贡献。另外,在最大贡献最大流中,我们可以把贡献的相反数存进去然后求最小费用最大流,最后取负即可。
最大权闭合子图模型
Description
首先我们讲讲闭合子图的概念。对于一张图 $G=(V,E)$,如果它的一个点集的子集 $V’$ 满足所有 $v\in V’$ 的出边都在 $V’$ 中,那么称这个子图是 $G=(V,E)$ 的一个闭合子图。而最大权闭合子图,就是给定每个点一个权值 $a_v$,要求最大化闭合子图的权值和。
Solution
首先注意,这个问题肯定不保证权值非负,否则直接全集就是最优解。考虑,选择一个集合也就等价于把所有的点分成两类,一类是选的,一类是不选的,并且其中选的有一部分是代价,有一部分是贡献。
具体做法是,把所有权值是正的点连到虚拟源点 $s$ 上,容量为 $a_v$,所有的权值是负的点都连到虚拟汇点 $t$ 上,容量是 $-a_v$。这有很大一个原因是网络流不允许负容量。另外,我们需要把所有 $(u,v)$ 的关系建立一条边,容量为 $INF$。然后,把所有的点分成两个部分,是不是就是把这个图割成两个分别与 $s$ 和 $t$ 相连的集合?于是,我们在这张图上跑最小割,再用所有正权和减去最小割就是答案。
考虑为什么是对的,首先,$(u,v)$ 的容量是 $INF$ 保证了我们不会割这一条边,也就是说,我们满足了 $(u,v)$ 不会被割这个条件。然后把这个东西割成了两个部分,我们把正权且与 $s$ 属于一个集合的点成为贡献点,负权与 $s$ 属于一个集合的叫做代价点,正权的与 $t$ 属于一个集合的叫做舍弃的贡献点,相应的,负权与 $t$ 相连的点叫做舍弃的代价点。那么,我们的最小割割的边不就是所有的舍弃的贡献点到 $s$ 的边和所有代价点到 $t$ 的边吗?而用所有正权点的权值和减去最小割,不就是减去不选的正权点,并且减去代价点吗?这就在感性上证明了为什么答案是对的。
最小路径覆盖
对于一张有向无环图(DAG) $G=(E,V)$,我们希望找到其中的 $m$ 跳路径 $e$,若每个路径的包含的点集为 $V_i$,则这 $m$ 条路径所包含的路径满足 $\bigcap\limits_{i=1}^m V_i=\emptyset$,$\bigcup\limits_{i=1}^m=V$,则称这个路径划分是 $G$ 的一个路径覆盖。而最小路径覆盖就是要求最小化 $m$ 的路径覆盖。
这里给一个结论:我们把每个点 $i$ 拆成两点 $i$ 与 $i+n$,然后对于原图上的 $e=(u,v)\in E$,在网络上连 $(u,v+n)$,$(s,i),(i+n,t),i\in [1,n]$,则最后最小路径覆盖=点数量-最大流。
证明
我们考虑反向合并。也就是说,我们先把每个点看成一条路径,这样路径就是 $n$ 条,我们要最小化路径数量,就可以在两条路径之间连边,也就是说,原本有路径 $u\to\dots\to x$ 和 $y\to\dots\to\ v$,而且正好有边 $x\to y$,于是我们可以合并两条路径变成 $u\to\dots\to x\to y\to\dots\to v=u\to\dots\to v$。这样我们就把需要的路径减少了一个,而我们要求的就变成了能减少的路径,或者说能合并的路径的数量。
于是考虑网络流,因为每个点只能够被一个点合并并且只能合并一个点,因此我们给每个点连边 $(s,i,1)$ 和 $(i+n,t,1)$ 表示每个点只能产生 $1$ 的贡献。然后每一个点可以选择合并的点都包含在 $E$ 中,只需要对于每一个 $(u,v)$,都连一条 $(u,v+n,1)$,就可以表示 $u$ 可以合并 $v$,最后跑出来就是可以合并的点的最大值。而拆点是因为我们总需要一个被合并和一个合并的点,如果不拆那么光是 $(s,i,1)$ 和 $(i,t,1)$ 两种边就可以把最大流拉到最大,变成 $n$ 了。
二分图最大匹配模型
首先,我们介绍二分图的基本概念。
对于图 $G=(E,V)$,我们把 $V$ 分成 $V_1$ 和 $V_2$ 使得 $V_1\cup V_2=V,V_1\cap V_2=\emptyset$,并且 $\forall e=(u,v)\in E$,都满足 $u,v$ 不在一个集合中,则称这张图是一张 二分图。而二分图最大匹配,就是在 $V_1,V_2$ 中找到一组对应关系,使得组数最多。其中一个对应关系可以表示为 $(u,v)$,其中 $u\in V_1, v\in V_2$ 并且存在 $e=(u,v)\in E$。而且每个点只能与一个点匹配。
为了解决这个模型,我们建立连边:
- $(s,u,1),u\in V_1$。
- $\forall e=(u,v)\in E,(u,v,1)$。
- $(u,t,1),u\in V_2$。
然后跑网络流最大流即可。
证明
题目中给出的约束无非以下几点:
- 每个点只能匹配一个点。
- 匹配的点之间必须有连边。
而对于第一个限制,我们让所有 $(s,u)$ 和 $(u,t)$ 容量都只有 $1$。对于第二个限制,我们只需要在建立连边的时候在两个有边的地方加入一条弧 $(u,v,1)$。
这样,这个网络的意义就是让每个点选择流向那个点,流过去就可以获得一点贡献,而且每个点只能流一遍。因此,我们流出的总流量就是二分图最大匹配。
例题选讲
P2774 方格取数问题
Description
有一个 $n\times m$ 的网格,每个格子中有一个权值 $a_{i,j}$。现在要求选择格子,并且相邻的格子不能被同时选择,求选择的最大权值和。
Solution
考虑这就是一个限制条件的网络流模型。具体地,它要求选择了 $(i,j)$ 之后就不能选择 $(i+1,j),(i-1,j),(i,j+1)$ 和 $(i,j-1)$。因此,可以套用最大权闭合子图模型。
具体地,我们发现如果把计 $sum=\sum\limits_{i=1}^n\sum\limits_{j=1}^ma_{i,j}$,那么它多算的部分就是所有的要选的 $(i,j)$ 周围的部分。而如果我们把周围的部分看成是负权值,也就代表了我们选择 $(i,j)$ 就必须选择它四周的点,而这些点权值为负,就相当于减去了这些点。因此使用最大权闭合子图模型即可。
1 | queue<int> q; |
