后缀数组 Created 2024-04-18 | Updated 2024-04-18
| Post Views:
后缀数组 这真的是一个极其恶心而又难以理解的东西。
定义 首先,对于一个字符串 $s=s[1\dots n]$,一个后缀 $i$ 被定义为 $s[i\dots n]$。
我们记录两个数组 $sa$ 和 $rk$,分别表示:
$sa_i$ 表示对所有后缀排序之后,第 $i$ 名的后缀下标是多少。
$rk_i$ 表示对所有后缀排序之后,后缀 $i$ 的排名是多少。
其中 $sa$ 被成为后缀数组。
由此我们不难看出,如果将 $sa$ 和 $rk$ 看成两个函数,其中 $f(x)=sa(x)$,那么 $f^{-1}(x)=rk(x)$。也就是说,他们两个互为反函数。
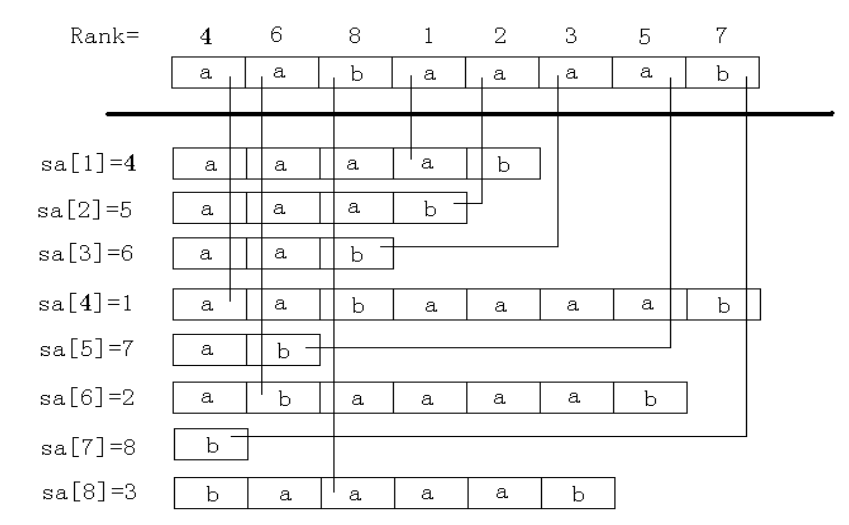
下面给出一张图来方便理解这个两个数组:
对于字符串 $s=\text{“aabaaaab”}$,它的所有后缀可以表示为 $\text{aabaaaab}$,$\text{abaaaab}$,$\text{baaaab}$,$\text{aaaab}$,$\text{aaab}$,$\text{aab}$,$\text{ab}$,$\text{b}$。将它们按照字典序排序,那么不难得到排序后的结果即为上图所示。
算法 朴素算法 我们可以 $O(n^2)$ 把每个后缀都存储下来,然后 $O(n^2\log n)$ 进行排序,这样就很容易得到这两个数组,但这样的复杂度显然不能够让我们满意,我们考虑优化。
朴素倍增 考虑先按照一个字母把原字符串排序,那么得到顺序之后,我们再把两个相邻的字符拼接起来,以第一个字符的排名为第一关键字,第二个为第二关键字,那么这个排序的过程和我们直接比较字符串大小便完全一样。这是因为字符串字典序的比较也是以第一个字符为第一关键字,第二个字符为第二关键字,第 $i$ 个字符为第 $i$ 关键字进行的。而对于长度不够的情况,直接让它等于 $-\infty$,这样就可以直接比较出来。
在排出结果之后,我们及时求出 $sa$ 和 $rk$,意义同上。
继续推广,我们已经知道了往后两个字符的排序,那么同理,对于每个位置 $i$,以 $rk_i$ 为第一关键字,以 $rk_{i+2}$ 为第二关键字进行排序。这样的排序也和直接比较四个字符是等价的,这样,记录 $rk$ 和 $rk$ 之后,我们就得到了四个字符的后缀数组。
继续递推。我们假设已经求到了每个位置之后 $2^{\omega}$ 的答案,那么我们以 $rk_i$ 为第一关键字,以 $rk_{i+2^{\omega}}$ 为第二关键字排序,得到的就是 $i$ 往后 $2^{\omega+1}$ 的答案。这样,我们倍增下去,就可以得到 $i$ 后面 $n$ 的答案。
还是放一张图让大家理解一下:
(我觉得这个方法就可以通过大部分题目了,尽管它有两只 $\log$)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 char c[N];int n, sa[N], rk[N], oldrk[N], w;bool cmp (int x,int y) return rk[x]==rk[y]?rk[x+w]<rk[y+w]:rk[x]<rk[y]; } signed main () ios::sync_with_stdio (false ); cin.tie (0 ), cout.tie (0 ); cin>>c+1 ; n=strlen (c+1 ); for (int i=1 ;i<=n;++i) rk[i]=c[i], sa[i]=i; for (w=1 ;w<n;w<<=1 ){ sort (sa+1 ,sa+1 +n,cmp); memcpy (oldrk,rk,sizeof (oldrk)); for (int p=0 , i=1 ;i<=n;++i) if (oldrk[sa[i]]==oldrk[sa[i-1 ]]&&oldrk[sa[i]+w]==oldrk[sa[i-1 ]+w]) rk[sa[i]]=p; else rk[sa[i]]=++p; } for (int i=1 ;i<=n;++i) cout<<sa[i]<<" " ; return 0 ; }
注意事项
这里的排序代码 sort(sa+1,sa+1+n,cmp) 中,数组 $sa$ 并不影响排序结果。也就是说,只要任意一个数组是 $sa$ 的一个排列,那么它就可以得到正确结果。这是因为主导排序结果的是 $rk$ 而非 $sa$。
$n\log n$ 优化。 优化很简单,把排序换成基数排序即可。
不会基数排序的可以看看我其它的 $\text{blog}$。
(这里直接放 $\text{oi-wiki}$ 的代码,因为我只写了常数优化之后的 $QwQ$)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 #include <algorithm> #include <cstdio> #include <cstring> #include <iostream> using namespace std;const int N = 1000010 ;char s[N];int n, sa[N], rk[N << 1 ], oldrk[N << 1 ], id[N], cnt[N];int main () int i, m, p, w; scanf ("%s" , s + 1 ); n = strlen (s + 1 ); m = 127 ; for (i = 1 ; i <= n; ++i) ++cnt[rk[i] = s[i]]; for (i = 1 ; i <= m; ++i) cnt[i] += cnt[i - 1 ]; for (i = n; i >= 1 ; --i) sa[cnt[rk[i]]--] = i; memcpy (oldrk + 1 , rk + 1 , n * sizeof (int )); for (p = 0 , i = 1 ; i <= n; ++i) { if (oldrk[sa[i]] == oldrk[sa[i - 1 ]]) { rk[sa[i]] = p; } else { rk[sa[i]] = ++p; } } for (w = 1 ; w < n; w <<= 1 , m = n) { memset (cnt, 0 , sizeof (cnt)); memcpy (id + 1 , sa + 1 , n * sizeof (int )); for (i = 1 ; i <= n; ++i) ++cnt[rk[id[i] + w]]; for (i = 1 ; i <= m; ++i) cnt[i] += cnt[i - 1 ]; for (i = n; i >= 1 ; --i) sa[cnt[rk[id[i] + w]]--] = id[i]; memset (cnt, 0 , sizeof (cnt)); memcpy (id + 1 , sa + 1 , n * sizeof (int )); for (i = 1 ; i <= n; ++i) ++cnt[rk[id[i]]]; for (i = 1 ; i <= m; ++i) cnt[i] += cnt[i - 1 ]; for (i = n; i >= 1 ; --i) sa[cnt[rk[id[i]]]--] = id[i]; memcpy (oldrk + 1 , rk + 1 , n * sizeof (int )); for (p = 0 , i = 1 ; i <= n; ++i) { if (oldrk[sa[i]] == oldrk[sa[i - 1 ]] && oldrk[sa[i] + w] == oldrk[sa[i - 1 ] + w]) rk[sa[i]] = p; else rk[sa[i]] = ++p; } } for (i = 1 ; i <= n; ++i) printf ("%d " , sa[i]); return 0 ; }
注意事项
这里每一次计数排序一定要倒序遍历数组,否则会产生一些奇妙的小错误。
这里在基数排序时,下标需要使用 $id_i$。当然,除了 sa[cnt[rk[id[i]]]--]=id[i] 这里面的 $id$ 之外,都写成 $i$ 也是可以的。
常数优化 第二关键字无需排序 我们在上一轮排序的时候,已经将 $2^{\omega-1}$ 的长度排过序了。因此,我们完全可以省略第一次排序的过程,直接将原来的后缀数组按照原顺序放入即可。值得注意的是,这里后 $\omega$ 个字符是没有第二关键字的,也就是说,它们的第二关键字是负无穷。因此,我们需要把它们提到最前面。
1 2 3 for (i=n, p=0 ;i>n-w;--i) id[++p]=i;for (i=1 ;i<=n;++i) if (sa[i]>w) id[++p]=sa[i]-w;
后面一个 $for$ 循环表示,按照排名遍历,对于所有下标大于 $\omega$ 的都放到数组里面,这是因为小于等于 $\omega$ 的不能作为第二关键字。执行完这些操作之后,我们便已经得到第二关键字排序之后的数组下标 $id$。
基数排序值域缩减 显然,我们的值域 $m$ 是严格小于等于 $n$ 的。因此,我们可以把每一次的值域记录一下,看 $rk$ 到底到多少。然后在基数排序的时候就可以减少一些时间(虽然用处不大,会有其它严格 $O(n)$ 的拖后腿 $qwq$)。
减少不连续内存访问 在电脑内存中,我们的地址访问有一个 $nxt$ 指针来指到上一个或者下一个地址,这样的访问是极其快速的(至少比不连续的访问要快)。因此,我们可以把 $rk[id[i]]$ 存储下来(这个是用的很多的下标),来减少常数,尽管比较玄学。
使用函数 $cmp$ 来计算是否重复 对于我们比较的过程 oldrk[sa[i]]==oldrk[sa[i-1]]&&oldrk[sa[i]+w]==oldrk[sa[i-1]+w] 的过程,我们会不断来回调用 sa 和 oldrk。而如果我们写成函数:
1 2 3 inline bool cmp (int x,int y) return oldrk[x]==oldrk[y]&&oldrk[x+w]==oldrk[y+w]; }
然后在主函数调用的时候就是 cmp(sa[i],sa[i-1])。这样,我们访问顺序就变成了 sa 之后 oldrk。虽然也是玄学优化,但实测还是有一内内作用的。
最后我们就可以得到一份常数不小但也不是很大的做法。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 int n, id[N], sa[N], rk[N], oldrk[N], cnt[N], m=127 , p=0 , i, w, key[N];char c[N];inline bool cmp (int x,int y) return oldrk[x]==oldrk[y]&&oldrk[x+w]==oldrk[y+w];}signed main () ios::sync_with_stdio (false ); cin.tie (0 ), cout.tie (0 ); cin>>(c+1 ); n=strlen (c+1 ); for (i=1 ;i<=n;++i) ++cnt[rk[i]=c[i]]; for (i=1 ;i<=m;++i) cnt[i]+=cnt[i-1 ]; for (i=n;i;--i) sa[cnt[rk[i]]--]=i; for (w=1 ;p<n;w<<=1 , m=p){ memset (cnt,0 ,m*sizeof (int )); for (i=n, p=0 ;i>n-w;--i) id[++p]=i; for (i=1 ;i<=n;++i) if (sa[i]>w) id[++p]=sa[i]-w; for (i=1 ;i<=n;++i) ++cnt[key[i]=rk[id[i]]]; for (i=1 ;i<=m;++i) cnt[i]+=cnt[i-1 ]; for (i=n;i;--i) sa[cnt[key[i]]--]=id[i]; memcpy (oldrk+1 , rk+1 , n*sizeof (int )); for (i=1 , p=0 ;i<=n;++i) rk[sa[i]]=cmp (sa[i],sa[i-1 ])?p:++p; } for (int i=1 ;i<=n;++i) cout<<sa[i]<<" " ; cout<<endl; return 0 ; }
注意事项
对于循环 for(i=n,p=0;i>n-w;--i) 正序循环和倒序循环都可以。