树上分治
树上分治
点分治
基本思想
类似于链表中的二分,链表作为树的一种特殊形式,那么我们是否可以把链表中的二分扩展到树上,完成树上一些关于路径的问题呢?于是我们就引入了 点分治 这个算法。具体地,点分治是通过有一定技巧地枚举路径的必经点,然后不重不漏地计算出所有路径的贡献。
那么如果我们普通枚举,不仅时间复杂度会变成 $O(n^2)$,连正确性都很难保证,这是因为普通枚举很难保证不重不漏。但是点分治给出了一种方法,使得复杂度在 $O(n\log n)$ 的情况下能够正确的处理问题。
类比链表,链表是通过枚举中点来把需要枚举的区间分成等大的两份,再通过该点是否符合题意,结合整个决策的单调性来判断临界点,在严格 $O(\log n)$ 内解决问题。那么我们在点分治的时候能不能也找到一个方案使得每次至少将问题规模缩小一半呢?这不禁让我们联想到一个概念:树的重心。
树的重心
对于一棵树,若树上的一个点 $x$ 满足:对于 $\forall y$,都有 $mx_x\le mx_y$,则称点 $x$ 是该树的一个重心。
其中 $mx_u=\max\limits_{edge=(u,v)} siz_v$。
也就是说树的重心其实是最大子树大小最小的节点。通过定义,我们在树上节点 $n\rightarrow \infty$ 时能够证明一下几个性质:
性质 1
对于一棵树,若 $x$ 是树的重心,那么至少存在两个节点与 $x$ 直接相连。
证明 1
若 $x$ 是重心且只有一个节点与 $x$ 相连,那么设 $y$ 是那个节点,那么 $mx_y$ 的最大值也是 $mx_x-1$,因此 $y$ 更优。
性质 2
对于一棵树,如果 $x$ 是它的重心,那么对于 $\forall y\in son_x$ 都满足 $siz_y\le \frac{siz_x}{2}$。
证明 2
同样地,对于 $x$ 是树的重心,若存在它的一个儿子 $y$ 满足 $siz_y\ge \frac{siz_x}{2}$,不难得到 $siz_x-siz_y\le \frac{siz_x}{2}$,也就是说,整棵子树除去 $y$ 后的大小小于 $\frac{siz_x}{2}$,因此 $mx_y\le\min{siz_x-siz_y,siz_y-1}\le mx_x$,所以 $y$ 会比 $x$ 更优。
那么通过这两条性质,我们能够总结出复杂度对的原因:
对于一个根节点 $u$,在经过 $O(siz)$ 处理完当层的信息之后,我们进行递归时问题规模总会缩小一半,也就是说,它的递归层数最多为 $O(\log n)$ 次,每一次都会使用 $\sum siz_{root}$ 的复杂度处理信息,也就是 $O(n)$,于是复杂度就是 $O(n\log n)$。当然,复杂度也会出现处理一层是 $n\log n$ 的情况,但总体 $n\log^2 n$ 的复杂度也基本可以接受。
一种更好的理解方法是当树退化成链的时候它就是二分。
统计信息
在递归到一定层次的时候,我们需要维护当前层的信息。考虑怎么样维护信息能够保证不重不漏。
考虑如果维护的路径全部都在一个子树内部,那么递归到该子树的时候一定还会处理到这条边,因此我们只需要处理跨子树的边,换一种说法,就是经过根节点的边。这样也大大方便了我们的统计工作。我们只需要以 $root$ 为根节点,以已经处理过的根节点作为分界对子树内求出需要的信息即可。
因为经过根节点,因此路径可以分为由儿子朝根节点的上行边和由根节点到儿子的下行边。因此在处理路径的时候需要快速对这两种边进行匹配。在匹配的时候往往会用到双指针、李超线段树等技巧,这也大概是点分治唯一需要改改板子的地方。
基本流程
- 拿到根节点开始初始化要处理的信息。
- 处理出来根节点下的信息,并且进行匹配。
- 寻找每个子树的新的根节点并继续点分治,重复 1 过程。
点分树
对于树上关于路径单词路径的问题,我们可以使用点分治很好地完成,但是对于需要修改并且对此询问的的问题,并且要求在线的,我们就可以用点分树进行求解。
基本思路
对于多次询问,我们需要一遍又一遍地进行点分治,但是我们不难发现,处理重心的过程是会重复很多遍的。但对于修改操作,我们又不得不重新计算每个节点的贡献是多少。因此总需要每次重新点分治。
我们发现,对于一个点 $u$,需要用到 $u$ 点信息的地方只有所有包含 $u$ 的子树,也就是说,在点分治的过程中,由于树的结构不会改变,每次包含 $u$ 节点的子树也就不会改变,而且这个数量级是 $\log n$ 的。也就是说,改变一个点 $u$,受到影响的最多只有 $\log n$ 个点。
因此,很自然地,我们想到了维护点分树的结构。具体地,我们把原来的树进行重构,让一个节点的 $fa$ 为点分治过程中它的上一层重心。举个栗子:
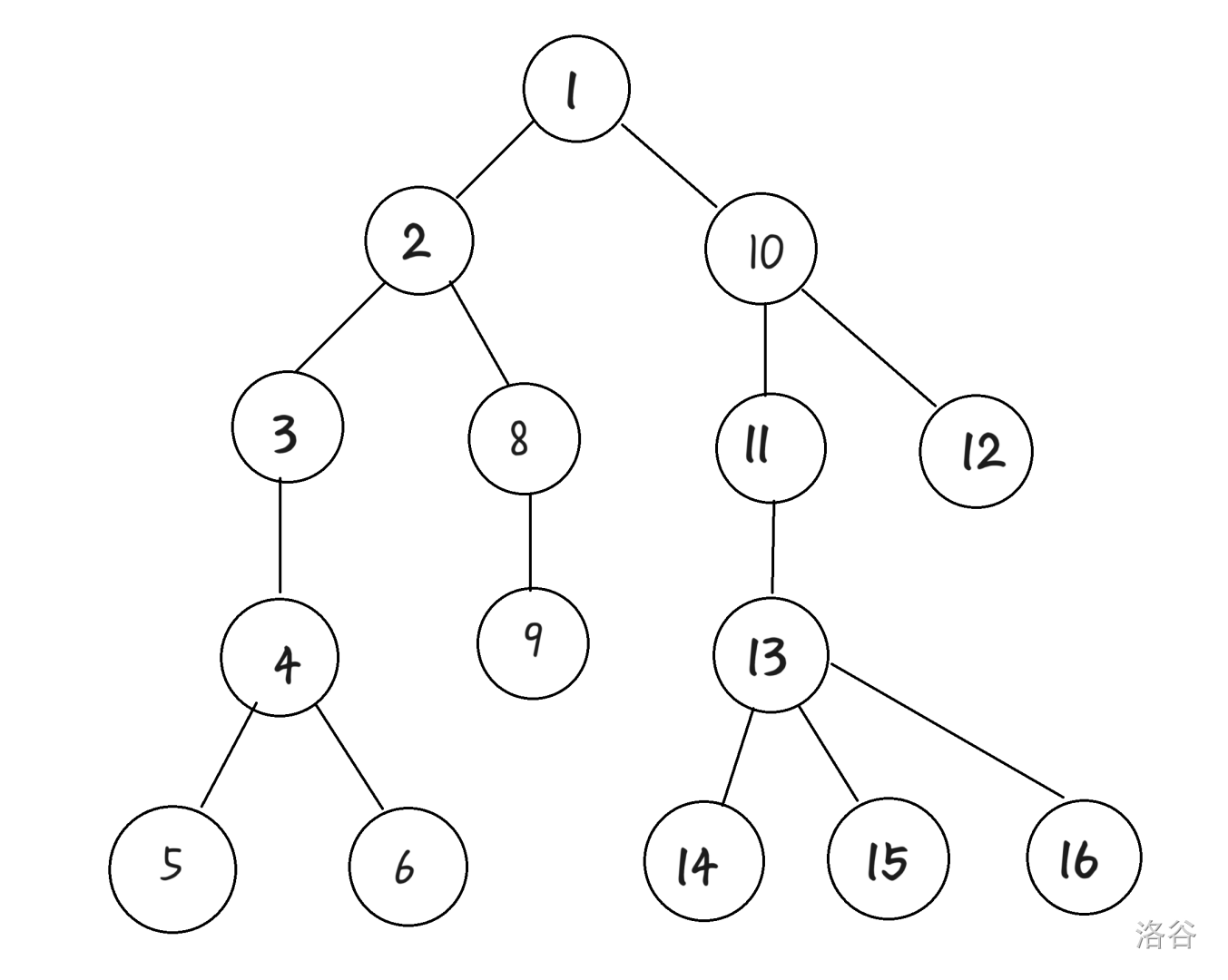
对于这个图,点分治的顺序是 $1, 3, 4, 5, 6, 8, 2, 9, 13, 10, 11, 12, 14, 15, 16$。于是,我们建立以下的 $fa$ 关系:
| 节点 | 1 | 2 | 3 | 4 | 5 | 6 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 父亲 | 0 | 8 | 1 | 3 | 4 | 4 | 3 | 8 | 13 | 10 | 10 | 11 | 13 | 13 | 13 |
这样,我们得到了每次点分治 一直遵循的递归顺序,这大大方便了我们模拟点分治的过程。于是,我们可以建出下图:
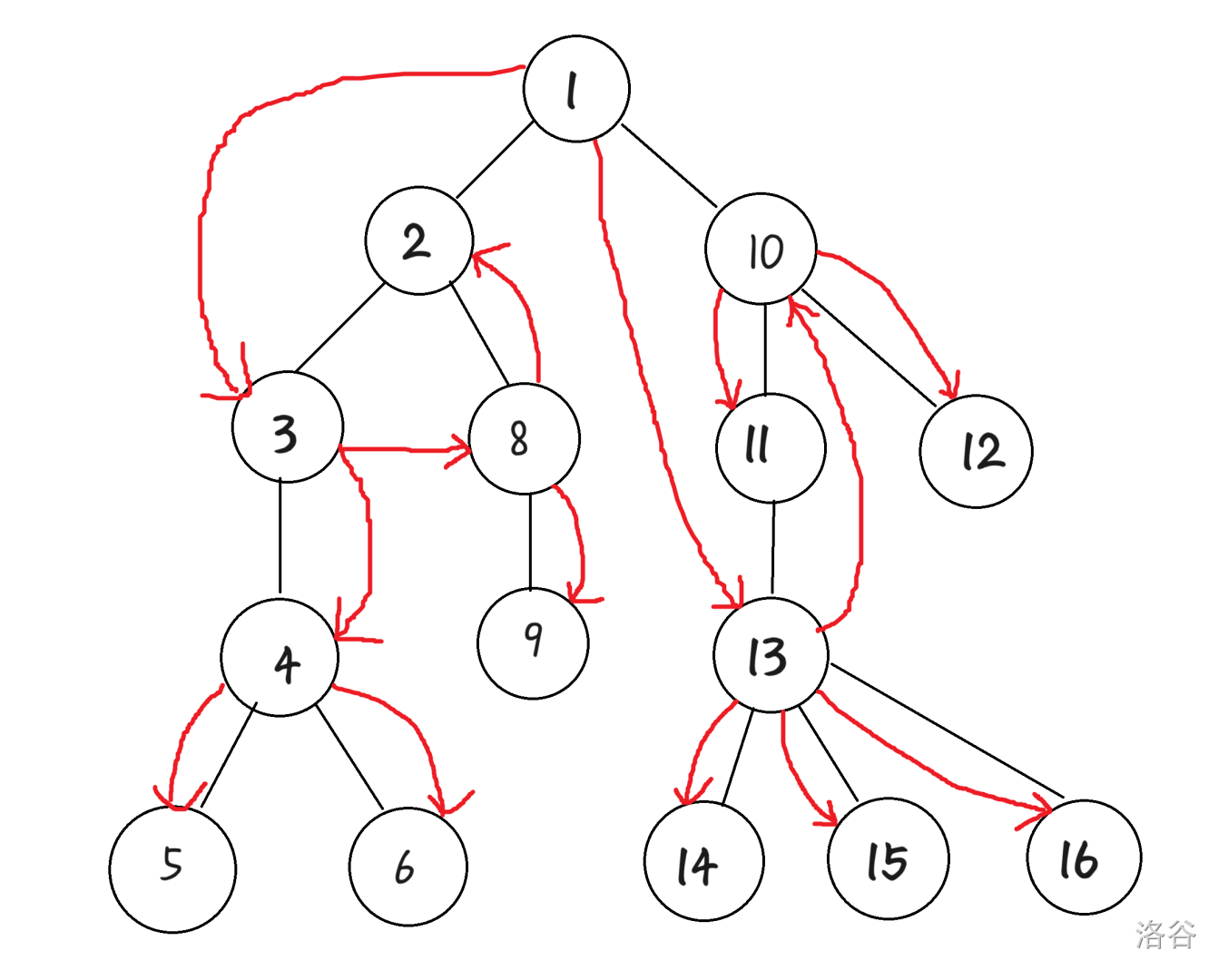
(红边是重构树上的边,黑色边是原来的边)
通过上述的分析以及我们的栗子可以得到以下两条性质:
性质 1
重构树的层数不超过 $\log n$。
这是一条显然的性质,已经在点分治中说明。但是这却可以引申出许多性质来帮助我们做题:
推论 1
如果我们维护 $n$ 个 vector,每个动态数组中存储所有儿子的信息,那么空间复杂度是 $O(n\log n)$。
证明 1
由于深度不超过 $\log n$,每个节点又只会被它的祖先统计到,因此每个节点最多被通缉 $\log n$ 次,也就是 $O(n\log n)$ 的空间复杂度。
于是,一些普通的树上很不对的 暴力 做法就可以在点分树上进行爬父亲操作一步步修改,只要单词修改复杂度可以接受,那么无非再加上一个 $\log$。
性质 2
对于原树上的两个点 $(u,v)$,它们在重构树上的最近公共祖先 $lca$ 一定在原树 $u\to v$ 的路径上。
证明 2
考虑在重构树上的最近公共祖先一定是把两个节点分到两个子树内的深度最低的那个点,也就是说,从此开始 $u,v$ 就不在一个子树内了。显然,只有 $u\to v$ 的路径上的节点可以做到这一点。
于是我们又可以得到一个重要推论:
推论 2
对于重构树上的两个点 $u,v$,若 $lca$ 为它们的最近公共祖先,它们在原树上的距离等于 $dis(u,lca)+dis(lca,v)$。
于是乎,我们对于点分树的基本思路已经掌握的差不多了,它基于点分治,支持单点修改和区间查询操作,复杂度一般在 $O(n\log^2 n)$ 量级。
模板题 P6329
题目传送门。
我们考虑在点分树上维护两个线段树,一个是 $t1[x][i]$ 表示与 $x$ 节点距离为 $i$ 的点的权值和。另一个 $t2[x][i]$ 表示 $x$ 节点在重构树上的子树内距离重构树上 $x$ 的父亲为 $i$ 的点的权值和。于是修改操作就是从 $x$ 开始,每次跳它重构树上的父亲,若 $x$ 与当前节点的距离 $dis$,则修改 $t1[x][dis]$,$t2$ 类比修改即可。对于查询操作,我们设 $x$ 与当前节点 $u$ 距离为 $dis$,那么就加上 $t1[u][k-dis]-t2[son][k-dis]$ 即可。其中 $son$ 表示 $u$ 在 $x$ 方向上的子树。这是因为 $x$ 方向上的子树内部已经被计算过了,需要容斥减掉。特别地,对于节点 $x$,直接加上 $t1[x][k]$ 即可。
关于为什么一定需要两个数组。很多学习者都会直觉性地认为 $x$ 到 $fa$ 无非就是多一个 $dis(x,fa)$,但别忘了,对于 $x$ 子树内的节点 $y$ 来说,$dis(fa,y)\not =dis(x,y)+dis(y,fa)$,因此需要另行计算。
初始化时,对于每个节点遍历它的子树,时间复杂度为 $O(n\log^2 n)$,然后一次修改或查询都是 $O(log^2 n)$ 的。因此总复杂度 $((n+m)\log^2 n)$。
注意,本题使用动态开点线段树时一定要计算好树的大小之后再进行 udpate,不要将范围设成 $[1,n]$,否则可能会被卡。
1 |
|
习题讲解
P3714 [BJOI2017] 树的难题
点分治+线段树
树上,路径问题,于是一眼点分治,这里维护的是不排序去重后的颜色价值和,求路径价值的时候非常容易,一遍 DFS 即可求出,但是考虑到根节点的颜色情况,我们不得不多记录一些东西。
首先,显然我们需要对于根节点到它的儿子路径上颜色相同的节点进行特殊处理,也就是,我们需要对于根节点到当前重心颜色一致的路径减去一遍该颜色的贡献,于是,我们考虑相同颜色放在一起讨论,于是就得到了第一步:
首先把 $u$ 的所有儿子按照颜色为第一关键字排序,以保证相同颜色在连续的区间内进行。
对于遍历到的当前颜色,我们需要开一棵线段树来维护它的最大值,然后对于全局(不包括该颜色),我们需要一颗线段树来维护最大值,于是在查询的时候,就需要取两次 max:(这里需要规定范围在 $[l,r]$ 内,因此需要规定区间查询。)
1 | ans=max(ans,mx[sub[j]]+col.query(1,1,n,max(1ll,L-sub[j]),R-sub[j])-val[color]); |
注意,每一次处理完一个子树之后需要把该子树信息合并到该颜色的线段树中去,而且在该颜色处理完之后需要把贡献合并到当前重心上面去。并且一定注意每次精准清空所有数组!
这些大概就是本题思路,但是本题思路不难,只要想到排序就会了,但是代码极其难写,我写了两个版本,第一个版本不知道为啥莫名其妙地 $\text{MLE}$,极其烦人,下面强调几个易错点:
- 线段树的范围一定要写对,最好是在区间 $[1,maxdep]$ 上进行存储,当然直接 $[1,n]$ 也问题不大。注意一定是 $1ll$ 与 $L-sub[j]$ 取
max而非 $0$,否则可能会导致 $\text{TLE}$ 或 $\text{MLE}$。 - 精准清空的时候一定注意全部清空,仔细检查自己是否有遗漏数组忘记清空。对于线段树内清空也是如此。
- 所有的数组初始化的时候要初始化成 $-\infty$,包括
ans,否则会导致负数答案变成 $0$。
下面给出代码:(这个代码本来是 $90pts$,Wa on test #6,如果有大佬可以帮忙调一调,我是特判了第六个点过的/bx/bx)
1 |
|
P7215 [JOISC2020] 首都
点分治+队列优化暴力
首先考虑朴素暴力 $O(n^3)$ 做法。很容易想到,我们可以枚举首都的城市 $i$,然后找到所有 $i$ 节点,把路径上的节点的颜色再进行修改,直到不再包含需要修改的节点为止。显然枚举 $O(n)$,然后暴力修改是 $O(n^2)$ 的。
这里很多同学会进入一个误区,即我们只需要修改所有 $i$ 节点之间的路径,但这是一个明显的错误,下面的样例就可以解释这个问题:
1 | input: |
显然,如果我们只修改 $1$ 路径上的节点,我们只需要修改 $2$ 号颜色即可。因为 $1$ 的路径只有 $1\to 2\to 4$ 这一条,但是显然在这条路径上包含的 $2$ 节点需要修改的话会影响到 $5$ 号节点也进行修改,导致 $5$ 与 $1$ 也不在一个联通块上,因此我们还需要修改 $1\to 3\to 5$ 的路径上的 $3$ 号颜色。
考虑如何优化这个暴力。其实,对于如何修改,我们完全可以做到 $O(n)$,只不过上一个修改的办法太过于暴力。我们假设现在的根节点是 $u$,那么所有与 $u$ 相同颜色的节点到 $u$ 的路径总可以跳 $fa$ 跳到 $u$,因此,我们每次让 $u$ 跳一次 $fa$,如果 $fa$ 节点的颜色未被访问,直接将该颜色的所有节点都修改为 $u$ 的颜色,然后把所有节点都加入到待修改的队列之中。然后在队列中每次取队首重复这个操作,我们发现所有的节点都被我们包含进去了,而且每个节点至多进队出队一次,因此我们做到了 $O(n^2)$ 的暴力(恭喜拿到 ${\LARGE\mathcal{21}}$ 分的好成绩!)
但是,如果想要拿到全分,还需要一些性质。我们先看特殊性质,也就是树是一条链的时候,这个时候我们考虑贪心,因为对于不包含大区间的可行联通块,总是小区间不比大区间劣(这里 区间 指的是一种颜色的左右端点)。如果含有大区间颜色,那么它一定不比那个大区间的颜色更优,因为相当于需要改大区间,因此对于小区间内有大区间颜色的颜色我们可以直接扔掉不管。
这就给我们一个启示:在树上是不是也可以这样呢?
首先,为了在不爆复杂度的基础上进行暴力,想到的依然是点分治。对于当前重心 $u$,我们遍历它的每一个子树 $v$,如果子树 $v$ 中包含颜色 $col$,使得存在别的节点 $x$ 不在子树 $v$ 内,且 $color_x=col$,则显然需要修改的路径就恢覆盖到当前的重心 $u$,那么它一定不比 $u$ 更优,可以直接舍弃。如果没有这样的节点,那么可以直接暴力计算需要多大代价。
然而上述论证只证明了我们做的决策一定不劣,但不保证一定最优。因为点分治会遍历到每一个节点,尽管它为根节点的时候可能已经没有子树,但是这不妨碍我们假设它为首都时对代价的计算。或者说,跨子树的颜色我们一定可以在一个重心的时候求到这个答案。这就保证了该算法的正确性。时间复杂度严格 $O(n\log n)$,跑得真的很快!
这个题不像上个题那么恶心,但是仍然有许多细节需要注意,这里我就直接放代码吧:
1 |
|
