斜率优化
前情回顾
如果对于一个 1D/1D 动态规划,即状态一维且递推公式可以化简为 $f_i=\max{f_j+w(i,j)}$ 的形式的动态规划,这样的动态规划在 $w(i,j)$ 不含同时与 $i,j$ 相关的函数时可以使用单调队列优化,即可以写成
$$f_i=\max{f_j+h_i+g_j}=\max{f_j+g_j}+h_i$$
时可以使用单调队列优化。
但是,如果 $w(i,j)$ 中包含同时与 $i$ 和 $j$ 相关的项,在 $j$ 项一次的情况下,可以使用斜率优化来 $O(n)$ 或 $O(\log n)$ 地完成题目。
一般情况
对于一般式:
$$f_i=\max{f_j+h_i+g_j-k_ix_j}$$
我们首先去掉 $\max$:
$$f_i=f_j+h_i+g_j-k_ix_j$$
将只含有 $j$ 的移到等式左边,其它的移到等式右边:
$$f_j+g_j=k_ix_j-h_i+f_i$$
在转移 $i$ 项时,我们可以将只含 $i$ 的函数看成常常数,于是计 $b_i=-h_i+f_i$,然后又将只含有 $j$ 的函数看成变量,计 $y_j=f_j+g_j$,于是式子就变成了我们熟悉的一次方程的形式:
$$y_j=k_ix_j+b_i$$
其中 $k_i,b_i$ 为常量。
不难发现,我们想要最大化 $f_i$,就需要最大化 $b_i$,即最大化一次函数的截距。
考虑如果决策点又无穷多个,即在 $x<i$ 时 $x$ 是连续的,我们考虑什么时候取到截距的最大值。
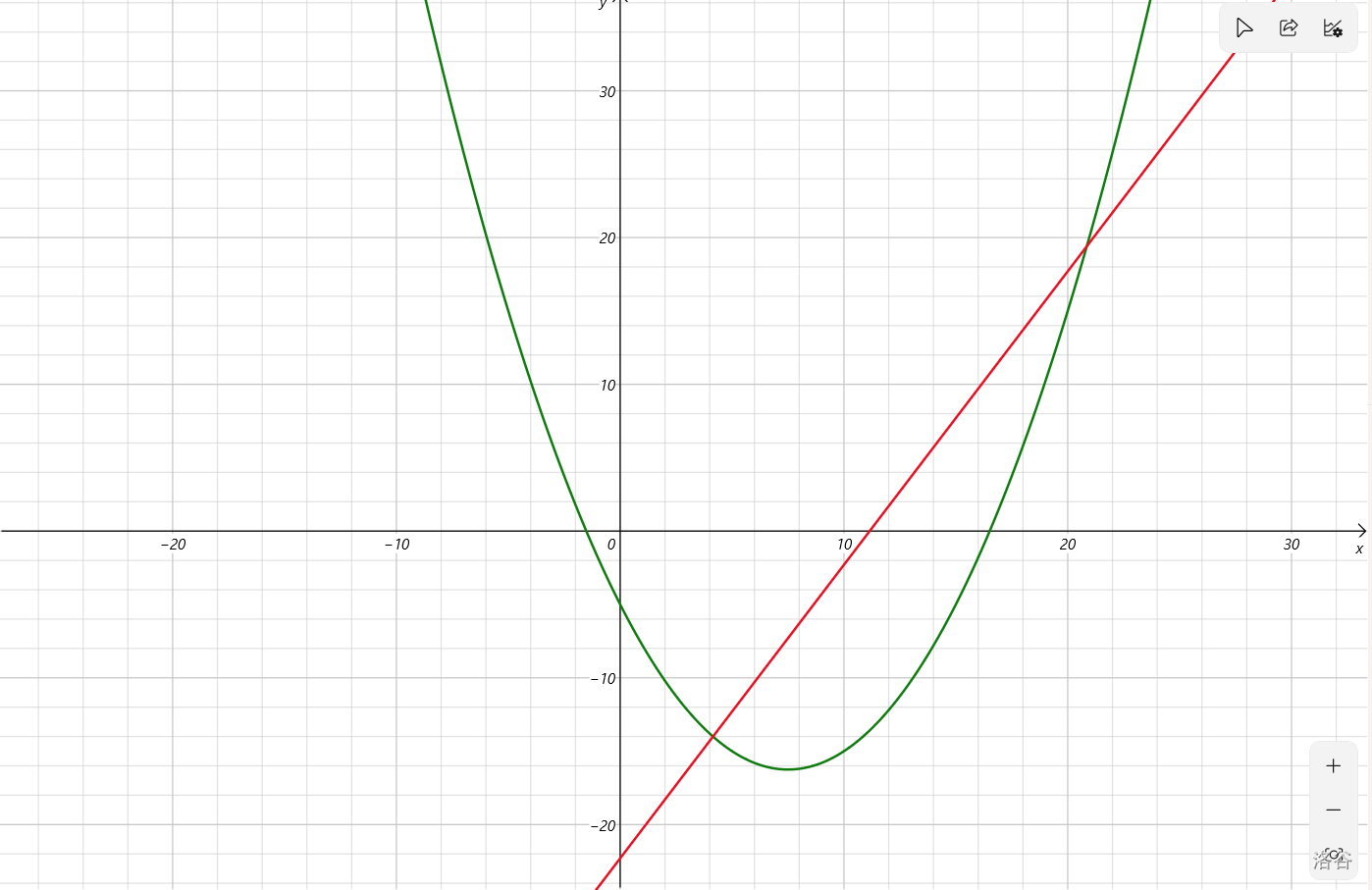
在这里,直线斜率 $k=2$,则在曲线上的一点 $(x_0,y_0)$ 可以把这个直线系唯一确定,即 $y=2x+y_0-2x_0$。显然,在直线与曲线相切的时候,即 $\frac{\mathrm{d}y}{\mathrm{d}x}=k$ 的时候,发现截距最小。
同理,不难推出,一条折线上的顶点 $(x_0,y_0)$,当它与前一个点的斜率 $k_1\le k$,且与它后一个点的斜率 $k_2\ge k$ 时,有截距的最小值。同时,向内凹的点是绝对不优的,这保证了斜率优化中斜率序列的单调性,因此一般地,我们可以使用二分查找来实现 $O(n\log n)$ 的转移。
但同时,如果我们的转移点的斜率单调递增,那么曾经被舍弃掉的 $k$ 再往后一定不会被用到,因此这类似于头出尾进的队列,同时对内元素单调,很自然想到用单调队列继续优化成 $O(n)$。
(Warning!!!) 注意事项
- 再队列中存储的是下标编号,一定再访问时访问
q[head]和q[tail],并且在+1时在head或tail里面加,如q[head+1]。 - 二分时比较
slope的时候一定要mid与mid+1的斜率与给定斜率比较。 double有时候会被良心出题人卡精度,因此在比较斜率的时候,当 $x$ 自变量单调递增,完全可以将分母乘到对面进行乘法的比较。- 在横坐标相等的时候注意特判,返回
sgn(Y(y)-Y(x))*INF。 - 注意横纵坐标范围会不会爆
double($15-16$ 位),如果爆了需要把返回类型改成long long,只保留一个函数是double。
习题讲解
洛谷 P3648 序列分割
Description
有序列 $a_n$,要求在这个序列里切 $k$ 刀,每次切会产生两边的联通块的和的乘积的贡献,求最大的贡献,并给出方案。
Solution
首先,一个结论是对于一个切的位置的集合,切的顺序是不重要的。
证明
首先,对于三个点 $x,y,z$,切两刀,$(x+y)\times z+x\times y=$,而 $x\times(y+z)+y\times z=x\times y+x\times z+y\times z$。
于是,若 $n$ 个数是可以的,那么无论第 $n+1$ 刀在最后切显然可以。若在倒数第二刀,那么与原来最后两刀构成三刀关系。以此类推,最后一刀在什么时候切都可以。
根据数归,证毕。
下面是推式子时间:
首先设出状态:$f_{i,j}$ 表示在 $i$ 与 $i+1$ 之间切第 $j$ 刀的最大贡献。
不难写出方程式:
$$f_{i,k}=\min\limits_{j=k-1}^{i-1}{f_{j,k-1}+(s_i-s_j)*(s_n-s_i)}$$
其中 $s_i=\sum\limits_{j=1}^i a_j$。去掉 $\min$ 并拆开柿子得到:
$$f_{i,k}=f_{j,k-1}+s_is_n+s_is_j-s_ns_j-s_i^2$$
将 $k$ 这一维滚掉(上一维用 $g_i$ 表示),并且移项得到:
$$g_j-s_ns_j=-s_is_j+s_i^2+f_i-s_is_n$$
计 $K(i)=s_i,X(j)=s_j,Y(j)=g_j-s_ns_j,B(i)=s_i^2+f_i-s_is_n$,于是得到:
$$Y(j)=K(i)X(j)+B(i)$$
然后就可以愉快地斜率优化啦。
这个题需要注意几点:
- 当 $X(x)=X(y)$ 时返回 $sgn(Y(y)-Y(x))*\infty$
double最多只能到整型的 $15-16$,可能会爆掉,因此Y函数需要改成long long类型。
Code
1 | double X(int x){ return s[x];} |
P5785 [SDOI2012] 任务安排
Description
给定序列 $F_n,T_n$,求划分方案 $a_k$ 表示把 $a_k$ 与 $a_{k}+1$ 分到两个方案,最小化答案
$$\sum\limits_{i=1}^k(\sum\limits_{j=a_{i-1}}^{a_i}F_j)(s\times i+\sum_{j=1}^{a_i}T_i)$$
Solution
容易想到,计前缀和 $f_i=\sum\limits_{j=1}^iF_i,t_i=\sum\limits_{j=1}^iT_i$,于是式子变成
$$\sum\limits_{i=1}^k(f_{a_i}-f_{a_{i-1}})(s\times i+t_{a_i})$$
设 $dp_i$ 表示分到第 $i$ 个数的最小费用,不难得出转移方程
$$dp_i=\min\limits_{j=1}^{i-1}{dp_j+(f_i-f_j)(c_i\times s+t_i)}$$
同样操作,去掉 $\min$ 并拆开式子得到:
$$dp_i=dp_j+f_ic_is+f_it_i-f_jc_is-f_jt_i$$
但是式子里面有一个很烦人的 $c_i$,它表示这个东西是第几组,会影响到 $f_j$ 的选取。但是仔细想想,似乎我们在完成一次分组后就会把后面所有的数都再乘上 $s$,因此我们不妨在 $dp_i$ 加上 $(f_n-f_i)\times s$,这样后面的就提前加进去了,于是得到:
$$dp_i=dp_j+f_is+f_it_i-f_js-f_jt_i+(f_n-f_i)\times s$$
移项可以得到:
$$dp+j-f_js=t_if_j+dp_i-f_is-f_it_i-(f_n-f_i)*s$$
按照套路,计 $Y(j)=dp+j-f_j,X(j)=f_j,K(i)=t_i,B(i)=dp_i-f_is-f_it_i-(f_n-f_i)*s$,柿子变成:
$$Y(j)=K(i)X(j)+B(i)$$
愉快地开始斜率优化。但这里注意,斜率 $K(i)$ 并不一定单调递增,于是我们需要二分来查找答案,使用单调栈来维护凸包。
Code
1 | double X(int x){ return f[x];} |
